Do not act on this article unless you are prepared to trash your disks, or if you are absolutely sure you understand what you are doing. Messing with raw disk sectors is risky!
VirtualBox allows us to use a disk device directly, rather than using a file as a virtual volume. For me, since I have two SSDs in my laptop, it meant I could tinker with virtual machines without risking my Windows 7 partition, while also being able to boot the VMs on real hardware if I wanted.
I never fully got my head around VMDK formats for RAW devices when using multiple independent partitions (e.g. one for each VM) on the disk – it’s hard to experiment on physical disks without risking disaster.
The knowledge that I was missing is that the partition layout of the disk is largely irrelevant. What we define in a virtual disk is the virtual sector list, known as ‘extents’ and, for each extent, where the real sector data resides (filesystem, raw disk sectors, or simply zeros). VBoxManage uses the partitioning information when creating raw disks to determine the sectors required when creating the VMDK file using the CLI. The sector count and offset values in the VMDK therefore reflect the partition layout by default.
However, you can specify any sector range from a physical disk as being the source data for an extent in your virtual disks. Make sure that the all disk definitions backed by raw sectors are defined as ‘shareable’ in the Virtual Media Manager, otherwise you’ll find one VM can block the others from starting, because it effectively has an exclusive lock on the physical disk.
A worked example of my VMDK extents.
Part or all of a disk can be used as a RAW partition in a virtual machine. The VMDK file will define the sector layout of your virtual disk, as seen by the VM. This is defined as a list of ‘extents’ with access mode, size, type, physical device, and starting offset.
Below is the partitioning I have defined in the host. I use the whole disk for VMs, so none of these partitions are actually used for host filesystems. There is around 100GB of unpartitioned space on this 240GB disk.
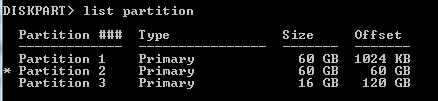
wmic:root\cli>partition get Name,NumberOfBlocks,StartingOffset
Name NumberOfBlocks StartingOffset
Disk #0, Partition #0 125829120 1048576
Disk #0, Partition #1 125829120 64425558016
Disk #0, Partition #2 33554432 128850067456The wmic output above shows the partitions, though gives the starting offset in bytes, so we need to divide these numbers by 512 to get the starting block offset (which gives 2048, 125831168, and 251660288 respectively).
Below is an snippet from one of my virtual disks – it’s physically primary partition 2 on the disk, exactly 60GiB in size. It has no access to any other sectors on the disk.
The virtual disk is backed by a 1MiB file (2048 sectors at physical offset 0) and a chunk of PhysicalDrive0 (125829120 sectors at physical offset 125831168), so the extent descriptions effectively concatenate the file and the physical disk sectors into a single virtual disk as seen by the VM.
# Extent description RW 2048 FLAT "Raw_Sectors_1MiB" 0 RW 125829120 FLAT "\\.\PhysicalDrive0" 125831168
In the lines above, taken from my vmdk file, line 2 defines a read-write area of the virtual disk that is 2048 sectors in length, starting at sector zero. It contains flat data, in other words raw sectors, and the sectors are stored in the file ./Raw_Sectors_1MiB. This allows a virtual disk to have its own partitioning and bootloader without messing up the contents of the main physical partition sectors (e.g. without it, the underlying partition would end up with an MBR/GPT etc., which would only make sense to a VM).
An empty file can be created with the following command, which in this case creates a 1MiB file to hold the 2048 sectors at the start of my virtual disk: –
fsutil file createnew Raw_Sectors_1MiB 1048576In line 3 of the extent descriptions, I define the next 125829120 sectors in the virtual drive as being backed by PhysicalDrive0 sectors starting at physical sector offset of 125831168. Since we are accessing the raw physical drive, we are paying no regard to the actual partitioning of the physical drive, so it’s important to make sure the physical sector offset and sector size are correct.
The information below shows what our virtual disk looks like to the guest, in this case booting from a live-cd.
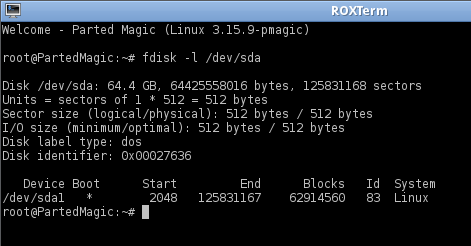
From the above fdisk output on the VM, we can see that the disk size is 125831168 sectors. This is exactly the sum of the sector sizes in the two extents defined above (2048 + 125829120).
Note that the disk size of 125831168 is coincidentally the same as the sector offset into the physical disk in the VMDK. This is because there happens to be a similar 60GiB partition preceding the one we’re using, which has a physical 2048 sectors preceding it (for partition alignment to a 1MiB boundary, as recommended). In short, the offset to our 1MiB + 60GiB partition is at the end of a 1MiB + 60GiB chunk of physical disk!
So, that was a short explanation of what it means to define a virtual disk from raw sectors on a host drive. This is the information I would have benefited from when reading the references below.
Breaking up the partition.
In this example, I will use the same partition, allocated equally across two virtual machines.
So, suppose I decide that 60GiB is too much for the VM I was creating, I decided to use half the partition for one VM’s disk, and the other half for another. I didn’t modify the disk’s partition table at all, I just allocated half the physical sectors to one virtual disk, and the other half to the another virtual disk. The extents were defined as follows.
# Extents for the first virtual disk on P2 RW 2048 FLAT "Raw_Sectors_1MiB" 0 RW 62914560 FLAT "\.\PhysicalDrive0" 125831168
# Extents for the second virtual disk on P2 RW 2048 FLAT "Raw_Sectors_1MiB" 0 RW 62914560 FLAT "\\.\PhysicalDrive0" 188745728
These are defined in different directories so each has its own Raw_Sectors_1MiB file for the first 2048 sectors. The second extent in both virtual disks is 62914560 sectors (30GiB), one backed by sectors at the start of partition 2 (125831168), and the other backed by sectors halfway through partition 2 (188745728).
Remember that any VMDK files that contain extents backed by the raw device must be marked Shareable in the Virtual Media Manager. You can check the value used by a VM by looking at its ‘.vbox’ file. The MediaRegistry will contain a HardDisk with type attribute, which should be ‘Shareable’.
I have deliberately not given the full files here because none of the other lines in a VMDK file are relevant outside of my system. However, it would be a simple task to automate the creation of VMDK files. As I understand it, the key values to vary between virtual disks is: –
- CID – this should be fffffffe to indicate a new disk.
- ddb.uuid.image – this UUID should be unique for each disk.
- The extent description size/physical sector offset.
I’ll end by saying that you really do have to follow the official docs when messing around with physical disks. Hopefully this will help a little in clarifying things, should you have the same unanswered questions that I had.
References
The VirtualBox documentation gives a lot of detail on how to configure RAW disk. You can read it here: http://www.virtualbox.org/manual/ch09.html#rawdisk
The libvmdk project has a detailed document that describes the VMDK file format. Not all the information will apply to the VirtualBox implementation, but what VirtualBox uses is documented clearly here: https://github.com/libyal/libvmdk/blob/master/documentation/VMWare%20Virtual%20Disk%20Format%20(VMDK).asciidoc
The VMDK Handbook Basics gives quite a lot of detail on the VMDK file format, though it was written for VMWare quite a while ago. Some of the the information may be outdated, or not applicable to VirtualBox.
